Ohmsches Gesetz für eine vollständige Kette und für einen Abschnitt einer Kette: Formeloptionen, Beschreibung und Erklärung

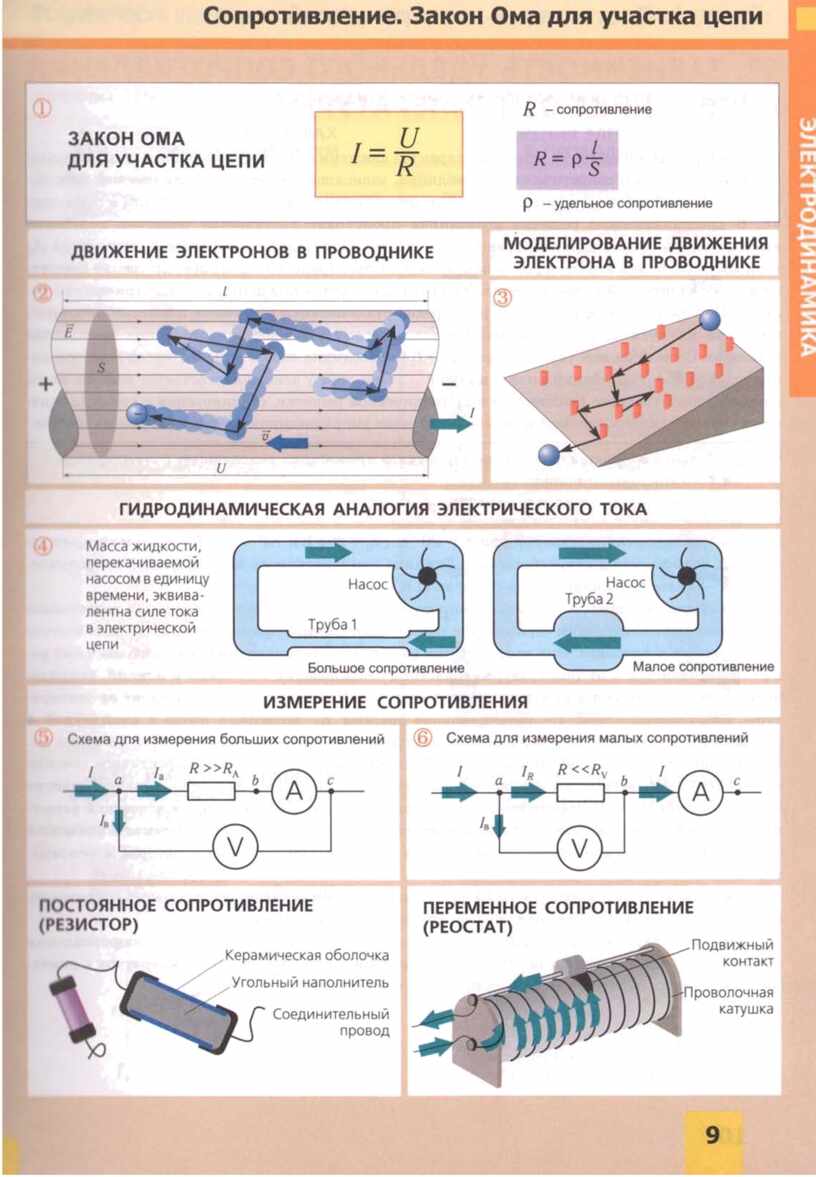
Für geschlossenen Kreislauf

Ein geschlossener Stromkreis bedeutet eine geschlossene elektrische Verbindung, durch die Strom fließt. Wenn es eine Reihe von Drähten gibt, die miteinander verbunden sind und den Stromkreis vervollständigen, so dass I von einem Ende des Kreises zum anderen verläuft, wird es ein geschlossener Stromkreis sein.

EMF (E) - wird in Volt bezeichnet und gemessen und bezieht sich auf die von einer Batterie oder Magnetkraft erzeugte Spannung gemäß dem Faradayschen Gesetz, das besagt, dass ein zeitlich veränderliches Magnetfeld einen elektrischen Strom induziert.

Dann: E = IR + Ir

E \u003d Ich (R + R)

Ich \u003d E / (R + R)

Wobei: r der Widerstand der Stromquelle ist.

Dieser Ausdruck ist als Ohmsches Gesetz der geschlossenen Regelkreise bekannt.

Heterogene Kette

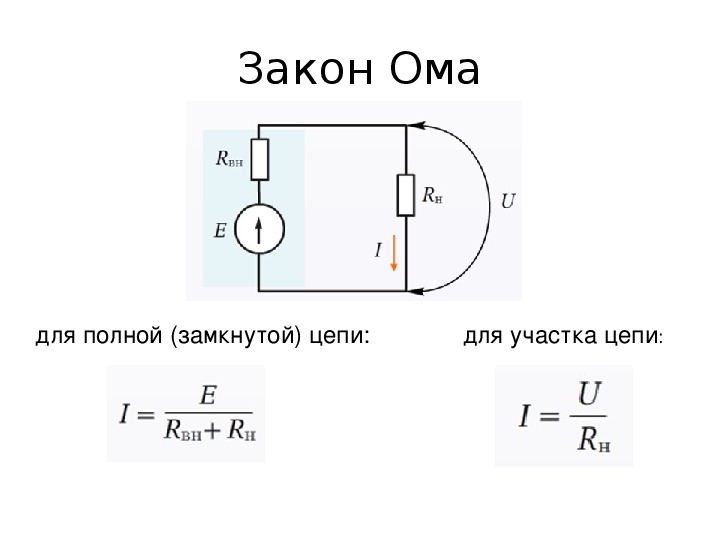
Separater Abschnitt und kompletter Stromkreis

Das Ohmsche Gesetz, angewendet auf einen Abschnitt oder den gesamten Stromkreis, kann in zwei Berechnungsmöglichkeiten berücksichtigt werden:

• Separater kurzer Abschnitt. Es ist Teil eines Stromkreises ohne EMF-Quelle.
• Eine vollständige Kette, die aus einem oder mehreren Abschnitten besteht. Dazu gehört auch eine EMF-Quelle mit eigenem Innenwiderstand.

Berechnung des aktuellen Abschnitts des Stromkreises

In diesem Fall wird die Grundformel I \u003d U / R angewendet, wobei I die Stromstärke, U die Spannung und R der Widerstand ist. Danach kann man die allgemein akzeptierte Interpretation des Ohmschen Gesetzes formulieren:

Diese Formulierung ist die Grundlage für viele andere Formeln, die auf der sogenannten "Kamille" im Grafikdesign vorgestellt werden. Im Sektor P wird die Leistung bestimmt, in den Sektoren I, U und R werden Aktionen in Bezug auf Stromstärke, Spannung und Widerstand durchgeführt.

Jeder Ausdruck - sowohl der grundlegende als auch der zusätzliche - ermöglicht es Ihnen, die genauen Parameter der Elemente zu berechnen, die für die Verwendung in der Schaltung vorgesehen sind.

Spezialisten, die mit elektrischen Schaltkreisen arbeiten, führen eine schnelle Bestimmung aller Parameter mit der in der Abbildung gezeigten Dreiecksmethode durch.

Die Berechnungen sollten den Widerstand der Leiter berücksichtigen, die die Elemente des Abschnitts verbinden. Da sie aus unterschiedlichen Materialien hergestellt sind, wird dieser Parameter in jedem Fall unterschiedlich sein.Wenn es notwendig ist, einen vollständigen Stromkreis zu bilden, wird die Hauptformel mit den Parametern einer Spannungsquelle, beispielsweise einer Batterie, ergänzt.

Berechnungsmöglichkeit für eine komplette Kette

Eine komplette Schaltung besteht aus einzelnen Abschnitten, die zusammen mit einer Spannungsquelle (EMK) zu einem Ganzen zusammengefügt werden. Somit wird der vorhandene Widerstand der Abschnitte um den Innenwiderstand der angeschlossenen Quelle ergänzt. Daher lautet die zuvor diskutierte Hauptinterpretation wie folgt: I = U / (R + r). Hier wurde bereits der Widerstandsindikator (r) der EMF-Quelle hinzugefügt.

Aus rein physikalischer Sicht wird dieser Indikator als sehr kleiner Wert angesehen. In der Praxis müssen Spezialisten dies jedoch bei der Berechnung komplexer Schaltungen und Schaltungen berücksichtigen, da zusätzlicher Widerstand die Genauigkeit der Arbeit beeinträchtigt. Zudem ist die Struktur der einzelnen Quellen sehr heterogen, wodurch sich der Widerstand teilweise in recht hohen Raten ausdrücken kann.

Die obigen Berechnungen werden in Bezug auf Gleichstromkreise durchgeführt. Aktionen und Berechnungen mit Wechselstrom erfolgen nach einem anderen Schema.

Die Wirkung des Gesetzes auf eine Variable

Bei Wechselstrom ist der Widerstand des Stromkreises die sogenannte Impedanz, bestehend aus aktivem Widerstand und reaktiver ohmscher Last. Dies ist auf das Vorhandensein von Elementen mit induktiven Eigenschaften und einem sinusförmigen Stromwert zurückzuführen. Auch die Spannung ist eine Variable, die nach eigenen Schaltgesetzen wirkt.

Daher wird das Design der Wechselstromschaltung nach dem Ohmschen Gesetz unter Berücksichtigung spezifischer Effekte berechnet: Voreilen oder Nacheilen der Größe des Stroms von der Spannung sowie das Vorhandensein von Wirk- und Blindleistung.Die Reaktanz umfasst wiederum induktive oder kapazitive Komponenten.

Alle diese Phänomene entsprechen der Formel Z \u003d U / I oder Z \u003d R + J * (XL - XC), wobei Z die Impedanz ist; R - aktive Last; XL, XC - induktive und kapazitive Lasten; J ist der Korrekturfaktor.

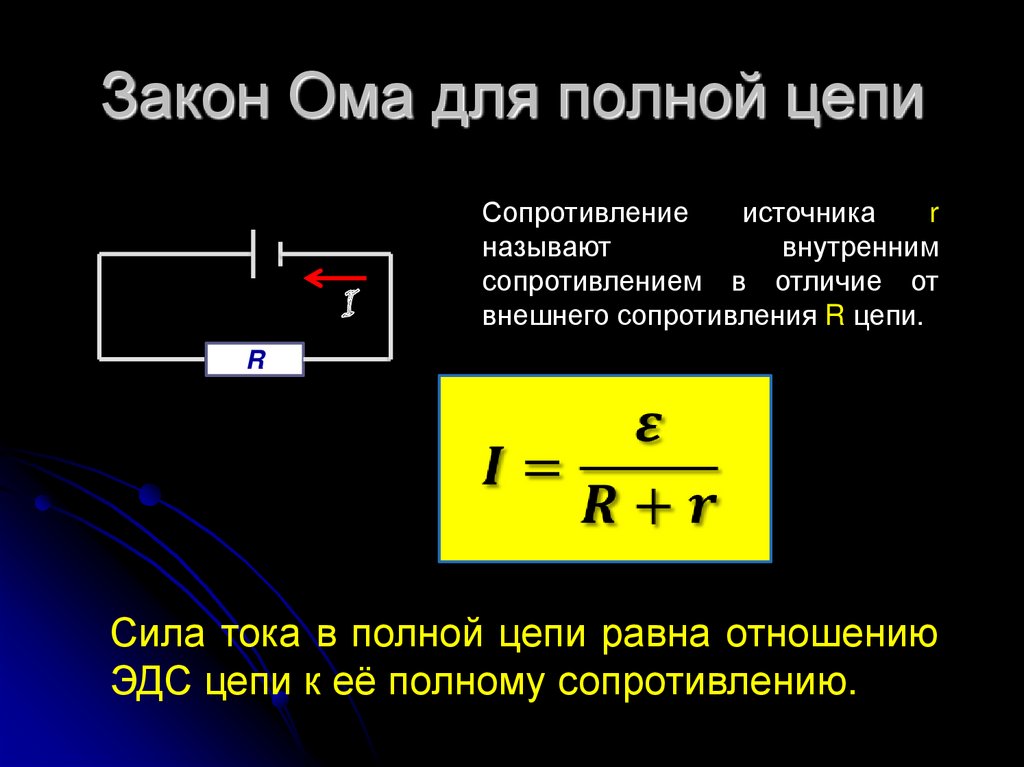
EMF-Quelle in einem vollständigen Stromkreis

Für das Auftreten von elektrischem Strom in einem geschlossenen Stromkreis muss dieser Stromkreis mindestens ein spezielles Element enthalten, in dem die Arbeit der Übertragung von Ladungen zwischen seinen Polen stattfindet. Die Kräfte, die Ladungen innerhalb dieses Elements tragen, tun dies gegen das elektrische Feld, was bedeutet, dass ihre Natur anders als elektrisch sein muss. Daher werden solche Kräfte als Dritte bezeichnet.

Reis. 1. Äußere Kräfte in der Physik.

Ein Element eines elektrischen Stromkreises, in dem äußere Kräfte wirken, um Ladungen gegen die Wirkung eines elektrischen Feldes zu übertragen, wird als Stromquelle bezeichnet. Sein Hauptmerkmal ist die Größe der äußeren Kräfte. Um es zu charakterisieren, wird ein spezielles Maß eingeführt - die elektromotorische Kraft (EMF), die mit dem Buchstaben $\mathscr{E}$ bezeichnet wird.

Der Wert der EMF der Stromquelle ist gleich dem Verhältnis der äußeren Kräfte für die Ladungsübertragung zum Wert dieser Ladung:

$$\mathscr{E}={A_{st}\über q}$$

Da die Bedeutung von EMF der Bedeutung von elektrischer Spannung sehr nahe kommt (erinnern Sie sich, Spannung ist das Verhältnis der vom elektrischen Feld, das die Ladung trägt, verrichteten Arbeit zum Wert dieser Ladung), wird EMF wie Spannung gemessen Volt:

$$1B={J\overCl}$$

Die zweitwichtigste elektrische Eigenschaft einer echten Stromquelle ist ihr Innenwiderstand.Wenn Ladungen zwischen den Anschlüssen übertragen werden, interagieren sie mit der Substanz der EMF-Quelle, und daher stellt die Quelle für elektrischen Strom auch einen gewissen Widerstand dar. Der Innenwiderstand wird wie der gewöhnliche Widerstand in Ohm gemessen, aber mit dem kleinen lateinischen Buchstaben $r$ bezeichnet.

Reis. 2. Beispiele für Stromquellen.

R - elektrischer Widerstand

Der Widerstand ist der Kehrwert der Spannung und kann mit der Wirkung verglichen werden, einen Körper in fließendem Wasser gegen eine Bewegung zu bewegen. Die Einheit von R ist Om, was mit dem griechischen Großbuchstaben Omega bezeichnet wird.

Der Kehrwert des Widerstands (1/R) ist als Leitfähigkeit bekannt, die die Fähigkeit eines Objekts misst, eine Ladung zu leiten, ausgedrückt in Siemens-Einheiten.

Die verwendete geometrisch unabhängige Größe heißt spezifischer Widerstand und wird üblicherweise mit dem griechischen Symbol r bezeichnet.

Weitere Informationen. Das Ohmsche Gesetz hilft dabei, drei wichtige Indikatoren für den Betrieb des Stromnetzes zu ermitteln, was die Berechnung der Leistung vereinfacht. Sie ist nicht auf einseitige Netzwerke mit Elementen wie Dioden, Transistoren und dergleichen anwendbar. Und es ist auch nicht auf nichtlineare Elemente anwendbar, von denen Thyristoren Beispiele sind, da sich der Widerstandswert dieser Elemente mit unterschiedlich gegebener Spannung und Strom ändert.

Bei höheren Frequenzen wird das verteilte Verhalten dominant. Dasselbe passiert bei sehr langen Stromleitungen. Selbst bei einer so niedrigen Frequenz wie 60 Hz hat eine sehr lange Übertragungsleitung, beispielsweise 30 km, eine verteilte Natur. Der Hauptgrund ist, dass die effektiven elektrischen Signale, die sich in Schaltkreisen ausbreiten, elektromagnetische Wellen sind, nicht Volt und Ampere, die von einer elektromagnetischen Welle infiziert werden.Die Leiter fungieren lediglich als Wellenleiter. So zeigt beispielsweise ein Koaxialkabel Z = 75 Ohm, selbst wenn sein Gleichstromwiderstand vernachlässigbar ist.

Das Ohmsche Gesetz ist das Grundgesetz der Elektrotechnik. Es hat eine Vielzahl praktischer Anwendungen in allen elektrischen Schaltungen und elektronischen Bauteilen.

Die häufigsten Beispiele für die Anwendung des Ohmschen Gesetzes:

1. Die an die elektrische Heizung gelieferte Leistung. Anhand des Widerstands der Heizspule und der angelegten Spannung kann die diesem Heizelement zugeführte Leistung berechnet werden.
2. Auswahl an Sicherungen. Sie sind Schutzkomponenten, die mit elektronischen Geräten in Reihe geschaltet werden. Sicherungen/CBs werden in Ampere bewertet. Der aktuelle Sicherungswert wird nach dem Ohmschen Gesetz berechnet.
3. Design elektronischer Geräte. Elektronische Geräte wie Laptops und Mobiltelefone benötigen eine Gleichstromversorgung mit einer bestimmten Nennstromstärke. Typische Mobiltelefonbatterien benötigen 0,7 bis 1 A. Ein Widerstand wird verwendet, um die Stromstärke zu steuern, die durch diese Komponenten fließt. Das Ohmsche Gesetz wird verwendet, um den Nennstrom in einer typischen Schaltung zu berechnen.

Die Schlussfolgerungen von Ohm wurden einst zu einem Katalysator für neue Forschungen auf dem Gebiet der Elektrizität, und heute haben sie ihre Bedeutung nicht verloren, da die moderne Elektrotechnik auf ihnen basiert. 1841 erhielt Om die höchste Auszeichnung der Royal Society, die Copley Medal, und der Begriff „Om“ wurde bereits 1872 als Einheit des Widerstands anerkannt.

Ungleichmäßiger Abschnitt des Gleichstromkreises

Eine heterogene Struktur hat einen solchen Abschnitt der Schaltung, in dem sich neben Leitern und Elementen eine Stromquelle befindet. Seine EMK muss bei der Berechnung der Gesamtstromstärke in diesem Bereich berücksichtigt werden.

Es gibt eine Formel, die die wichtigsten Parameter und Prozesse eines heterogenen Standorts definiert: q = q0 x n x V. Seine Indikatoren sind wie folgt gekennzeichnet:

• Beim Bewegen von Ladungen (q) erhalten sie eine bestimmte Dichte. Seine Leistung hängt von der Stromstärke und der Querschnittsfläche des Leiters (S) ab.
• Unter Bedingungen einer bestimmten Konzentration (n) ist es möglich, die Anzahl der Einheitsladungen (q0), die in einem einzigen Zeitraum bewegt wurden, genau anzugeben.
• Für Berechnungen wird der Leiter bedingt als zylindrischer Abschnitt mit einem gewissen Volumen (V) betrachtet.

Beim Anschließen des Leiters an die Batterie wird diese nach einiger Zeit entladen. Das heißt, die Bewegung der Elektronen verlangsamt sich allmählich und stoppt schließlich ganz. Dies wird durch das Molekülgitter des Leiters erleichtert, das der Kollision von Elektronen untereinander und anderen Faktoren entgegenwirkt. Um solche Widerstände zu überwinden, müssen zusätzlich bestimmte Kräfte Dritter aufgebracht werden.

Während der Berechnung werden diese Kräfte zu den Coulomb-Kräften addiert. Um eine Einheitsgebühr q vom 1. Punkt zum 2. zu übertragen, müssen außerdem die Arbeiten A1-2 oder einfach A12 ausgeführt werden. Dazu wird eine Potentialdifferenz (ϕ1 - ϕ2) erzeugt. Unter der Wirkung einer Gleichstromquelle entsteht eine EMF, die Ladungen entlang des Stromkreises bewegt. Die Größe der Gesamtspannung setzt sich aus allen oben angegebenen Kräften zusammen.

Die Polarität des Anschlusses an die DC-Versorgung muss bei den Berechnungen berücksichtigt werden. Wenn die Terminals geändert werden, ändert sich auch die EMF, was die Ladungsbewegung beschleunigt oder verlangsamt.

Serielle und parallele Verbindung von Elementen

Bei Elementen eines Stromkreises (Stromkreisabschnitt) ist ein charakteristisches Moment eine Reihen- oder Parallelschaltung.

Dementsprechend geht jede Verbindungsart mit einer anderen Art des Stromflusses und der Spannungsversorgung einher. Aus diesem Grund wird das Ohmsche Gesetz auch unterschiedlich angewendet, je nach Möglichkeit Elemente einzubeziehen.

Eine Kette von in Reihe geschalteten Widerstandselementen

In Bezug auf eine Reihenschaltung (Teil eines Stromkreises mit zwei Komponenten) wird die Formulierung verwendet:

• ich = ich₁ = ich₂ ;
• U = U₁ + u₂ ;
• R=R₁ +R₂

Diese Formulierung zeigt deutlich, dass unabhängig von der Anzahl der in Reihe geschalteten Widerstandskomponenten der in einem Abschnitt der Schaltung fließende Strom seinen Wert nicht ändert.

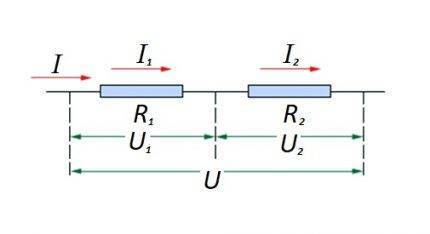Verbinden von Widerstandselementen in einem Schaltungsabschnitt in Reihe miteinander. Diese Option hat ein eigenes Berechnungsgesetz. Im Diagramm: I, I1, I2 - Stromfluss; R1, R2 - Widerstandselemente; U, U1, U2 - angelegte Spannung

Die an die aktiven Widerstandskomponenten der Schaltung angelegte Spannung ist die Summe und addiert sich zum Wert der EMF-Quelle.

In diesem Fall ist die Spannung an jedem einzelnen Bauteil: Ux = I * Rx.

Der Gesamtwiderstand sollte als Summe der Werte aller Widerstandskomponenten der Schaltung betrachtet werden.

Eine Kette parallel geschalteter Widerstandselemente

Im Falle einer Parallelschaltung von ohmschen Bauelementen gilt die Formulierung als fair im Hinblick auf das Gesetz des deutschen Physikers Ohm:

• ich = ich₁ + ich₂ … ;
• U = U₁ = u₂ … ;
• 1/R = 1/R₁ + 1 / R₂ + …

Möglichkeiten zur Zusammenstellung von Schaltungsteilen "gemischter" Art sind bei Verwendung von parallelen und seriellen Verbindungen nicht ausgeschlossen.

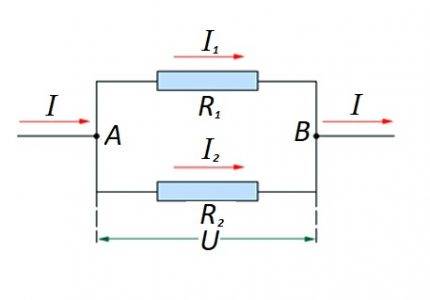Die Parallelschaltung von Widerstandselementen in einem Schaltungsabschnitt. Für diese Option wird ein eigenes Berechnungsgesetz angewendet. Im Diagramm: I, I1, I2 - Stromfluss; R1, R2 - Widerstandselemente; U - angelegte Spannung; A, B - Ein- / Ausstiegspunkte

Für solche Optionen wird die Berechnung normalerweise durch die anfängliche Berechnung der Widerstandsbewertung der Parallelschaltung durchgeführt. Dann wird der Wert des in Reihe geschalteten Widerstands zum Ergebnis addiert.

Integrale und differentielle Formen des Rechts

Alle oben genannten Punkte mit Berechnungen gelten für Bedingungen, bei denen Leiter mit einer sozusagen „homogenen“ Struktur als Teil elektrischer Schaltungen verwendet werden.

Mittlerweile hat man es in der Praxis oft mit dem Aufbau eines Schaltplans zu tun, bei dem sich die Struktur der Leiterbahnen in verschiedenen Bereichen ändert. Beispielsweise werden Drähte mit größerem Querschnitt verwendet oder umgekehrt kleinere auf Basis unterschiedlicher Materialien hergestellt.

Um solche Unterschiede zu berücksichtigen, gibt es eine Variation des sogenannten „Differential-Integral-Ohmschen Gesetzes“. Für einen unendlich kleinen Leiter wird die Stromdichte in Abhängigkeit von der Intensität und dem Leitfähigkeitswert berechnet.

Unter der Differentialrechnung wird die Formel genommen: J = ό * E

Für die Integralrechnung gilt jeweils die Formulierung: I * R = φ1 - φ2 + έ

Diese Beispiele sind jedoch eher der Schule der höheren Mathematik zuzuordnen und werden in der realen Praxis eines einfachen Elektrikers nicht wirklich verwendet.

Strom und Widerstand verstehen

Beginnen wir mit dem Konzept des elektrischen Stroms. Kurz gesagt, elektrischer Strom in Bezug auf Metalle ist die gerichtete Bewegung von Elektronen - negativ geladenen Teilchen. Sie werden normalerweise als kleine Kreise dargestellt.In einem ruhigen Zustand bewegen sie sich zufällig und ändern ständig ihre Richtung. Unter bestimmten Bedingungen - dem Auftreten einer Potentialdifferenz - beginnen diese Partikel eine bestimmte Bewegung in eine bestimmte Richtung. Diese Bewegung ist der elektrische Strom.

Um es klarer zu machen, können wir Elektronen mit Wasser vergleichen, das auf einer Ebene verschüttet wurde. Solange das Flugzeug stillsteht, bewegt sich das Wasser nicht. Aber sobald ein Hang auftauchte (ein Potentialunterschied entstand), begann sich das Wasser zu bewegen. Genauso ist es mit Elektronen.

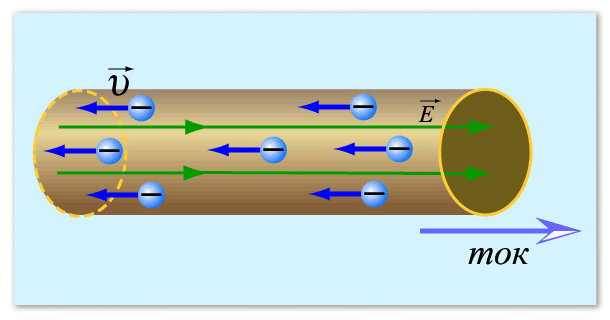
So kann man sich einen elektrischen Strom vorstellen

Jetzt müssen wir verstehen, was Widerstand ist und warum sie eine Rückkopplung mit der Stromstärke haben: Je höher der Widerstand, desto niedriger der Strom. Wie Sie wissen, bewegen sich Elektronen durch einen Leiter. Meist handelt es sich dabei um Metalldrähte, da Metalle Strom gut leiten können. Wir wissen, dass das Metall ein dichtes Kristallgitter hat: viele Teilchen, die eng beieinander liegen und miteinander verbunden sind. Elektronen, die sich zwischen Metallatomen bewegen, kollidieren mit ihnen, was ihre Bewegung erschwert. Dies hilft, den Widerstand zu veranschaulichen, den ein Leiter ausübt. Jetzt wird klar, warum je höher der Widerstand, desto geringer die Stromstärke - je mehr Teilchen, desto schwieriger ist es für Elektronen, den Weg zu überwinden, sie tun es langsamer. Das scheint geklärt zu sein.

Wenn Sie diese Abhängigkeit empirisch testen möchten, finden Sie einen variablen Widerstand, schalten Sie einen Widerstand - ein Amperemeter - eine Stromquelle (Batterie) in Reihe. Es ist auch wünschenswert, einen Schalter in die Schaltung einzufügen - einen gewöhnlichen Kippschalter.

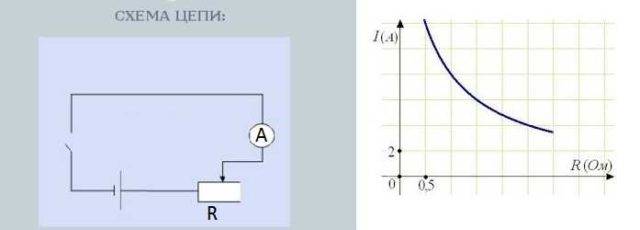
Schaltung zum Testen der Abhängigkeit des Stroms vom Widerstand

Durch Drehen des Widerstandsknopfs ändert sich der Widerstand.Gleichzeitig ändern sich auch die Messwerte des Amperemeters, das die Stromstärke misst. Je größer der Widerstand, desto weniger weicht der Pfeil ab - desto weniger Strom. Je niedriger der Widerstand, desto mehr weicht der Pfeil ab - der Strom ist größer.

Die Abhängigkeit des Stroms vom Widerstand ist nahezu linear, dh sie spiegelt sich in der Grafik als nahezu gerade Linie wider. Warum fast - das sollte separat besprochen werden, aber das ist eine andere Geschichte.

Ohmsches Gesetz für Wechselstrom

Bei der Berechnung von Wechselstromkreisen wird anstelle des Widerstandskonzepts das Konzept der "Impedanz" eingeführt. Die Impedanz wird mit dem Buchstaben Z bezeichnet und enthält den aktiven Widerstand der Last R_a und Reaktanz X (oder R_r). Dies liegt an der Form des sinusförmigen Stroms (und Strömen jeder anderen Form) und den Parametern der induktiven Elemente sowie den Schaltgesetzen:

1. Der Strom in einem induktiven Stromkreis kann sich nicht sofort ändern.
2. Die Spannung in einem Stromkreis mit einer Kapazität kann sich nicht sofort ändern.

Somit beginnt der Strom der Spannung nachzueilen oder vorzueilen, und die Scheinleistung wird in Wirk- und Blindleistung unterteilt.

U=I/Z

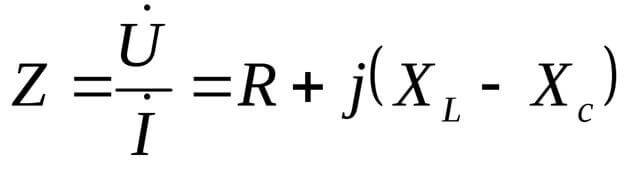
X_L und X_C sind die reaktiven Komponenten der Last.

Dazu wird der Wert cosФ eingeführt:

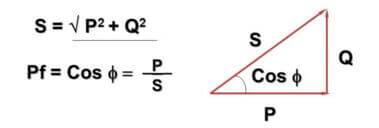
Hier - Q - Blindleistung aufgrund von Wechselstrom und induktiv-kapazitiven Komponenten, P - Wirkleistung (in aktiven Komponenten dissipiert), S - Scheinleistung, cosФ - Leistungsfaktor.

Sie haben vielleicht bemerkt, dass sich die Formel und ihre Darstellung mit dem Satz des Pythagoras überschneiden. Dies ist richtig und der Winkel Ф hängt davon ab, wie groß die reaktive Komponente der Last ist – je größer sie ist, desto größer ist sie. In der Praxis führt dies dazu, dass der tatsächlich im Netz fließende Strom größer ist als der von einem Haushaltszähler berücksichtigte, während Unternehmen für die volle Leistung bezahlen.

In diesem Fall wird der Widerstand in komplexer Form dargestellt:

Dabei ist j eine imaginäre Einheit, die typisch für die komplexe Form von Gleichungen ist. Weniger häufig als i bezeichnet, aber in der Elektrotechnik wird auch der Effektivwert des Wechselstroms bezeichnet, daher ist es, um nicht verwechselt zu werden, besser, j zu verwenden.

Die imaginäre Einheit ist √-1. Es ist logisch, dass es beim Quadrieren keine solche Zahl gibt, was zu einem negativen Ergebnis von "-1" führen kann.

Wenn das Ohmsche Gesetz eintritt

Optimale Bedingungen zu schaffen, ist nicht einfach. Auch in reinen Leitern ändert sich der elektrische Widerstand mit der Temperatur. Seine Abnahme minimiert die Aktivität der Moleküle des Kristallgitters, was die Bewegung freier Ladungen vereinfacht. Ab einem bestimmten Grad des "Einfrierens" tritt der Effekt der Supraleitung auf. Beim Erhitzen wird der gegenteilige Effekt (Verschlechterung der Leitfähigkeit) beobachtet.

Gleichzeitig behalten Elektrolyte, Metalle und bestimmte Keramikarten unabhängig von der Stromdichte ihren elektrischen Widerstand. Die Stabilität der Parameter bei Einhaltung eines bestimmten Temperaturregimes ermöglicht es, die Formeln des Ohmschen Gesetzes ohne zusätzliche Korrekturen anzuwenden.

Halbleitermaterialien und Gase sind durch unterschiedliche elektrische Widerstände gekennzeichnet. Dieser Parameter wird maßgeblich von der Stromstärke im Kontrollvolumen beeinflusst. Zur Berechnung der Leistungsmerkmale müssen spezielle Berechnungsverfahren angewendet werden.

Bei Berücksichtigung von Wechselstrom wird die Berechnungsmethode korrigiert. In diesem Fall muss das Vorhandensein reaktiver Komponenten berücksichtigt werden. Mit der Widerstandsnatur des Widerstands ist es möglich, die betrachteten Berechnungstechnologien basierend auf den Formeln des Ohmschen Gesetzes anzuwenden.

Kirchhoffsche Gesetze.

Verteilung
Ströme in den Zweigen des Stromkreises
gehorcht Kirchhoffs erstem Gesetz,
und die Verteilung der Spannungen über die Abschnitte
Die Kette gehorcht dem zweiten Kirchhoffschen Gesetz.

Kirchhoffsche Gesetze
zusammen mit dem Ohmschen Gesetz sind die wichtigsten
in der Theorie elektrischer Schaltungen.

Der Erste
Kirchhoffsches Gesetz:

Algebraisch
Die Summe der Ströme im Knoten ist Null:

_ich
= 0 (19)

Wo
ich
ist die Anzahl der Zweige, die an einem bestimmten Knoten zusammenlaufen.

Das heißt, Summation
erstreckt sich auf die Strömungen in den Zweigen,
die im Überlegten zusammenlaufen
Knoten.

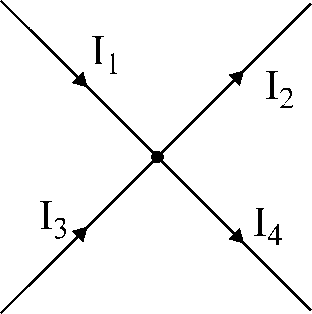
Abb.17. Illustration
zum ersten Kirchhoffschen Gesetz.

Nummer
Gleichungen nach der ersten zusammengestellt
Das Kirchhoffsche Gesetz wird durch die Formel bestimmt:

Nein
= Nu
– 1,

Wo
Nu
ist die Anzahl der Knoten in der betrachteten Kette.

Anzeichen für Strömungen
Gleichungen werden unter Berücksichtigung der ausgewählten berücksichtigt
positive Richtung. Zeichen bei
Ströme sind gleich, wenn die Ströme gleich sind
daran orientiert
Knoten.

Zum Beispiel,
für den in Abb. 17 gezeigten Knoten:
Wir weisen den zum Knoten fließenden Strömen Vorzeichen zu
"+" und zu den vom Knoten fließenden Strömen - Zeichen
«-».

Dann die Gleichung
nach Kirchhoffs erstem Gesetz wird es geschrieben
So:

ich₁
- ICH₂
+ ich₃
- ICH₄
= 0.

Gleichungen,
erstellt nach Kirchhoffs erstem Gesetz,
werden Knoten genannt.

Dies
das Gesetz drückt die Tatsache aus, dass im Knoten
elektrische Ladung sammelt sich nicht an
und wird nicht verbraucht. Die Menge an elektr
Gebühren, die auf die Website kommen, entsprechen der Summe
Ladungen, die den Knoten in ein und demselben verlassen
gleiche Zeitspanne.

Zweite
Kirchhoffsches Gesetz:

Algebraisch
Summe von emk in jedem geschlossenen Kreislauf
Kette ist gleich der algebraischen Summe der Fälle
Spannung an den Elementen dieser Schaltung:

Ui
= 
Ei

IiRi=Ei(20)

Wo
ich
- Elementnummer (Widerstand bzw
Spannungsquelle) in der betrachteten
Kontur.

**Nummer
Gleichungen nach dem zweiten zusammengestellt
Das Kirchhoffsche Gesetz wird durch die Formel bestimmt:

Nein
= Nb
- Nu
+ 1 – Ned.s.

Wo
Nb
- die Anzahl der Abzweigungen des Stromkreises;

Nu
— Anzahl der Knoten;

Ned.s.
ist die Anzahl der idealen EMK-Quellen.

Abb.18. Illustration
zum zweiten Kirchhoffschen Gesetz.

Zum,
das zweite Gesetz richtig zu schreiben
Kirchhoff für eine gegebene Kontur folgt
folgende Regeln einhalten:

1. willkürlich
   wählen Sie die Richtung der Konturumfahrung,
   zum Beispiel im Uhrzeigersinn (Abb. 18).

2. emf
   und Spannungsabfälle, die übereinstimmen
   in die Richtung mit der ausgewählten Richtung
   bypass werden in einem Ausdruck mit geschrieben
   Zeichen "+"; wenn e.f.s. und Spannungsabfall
   stimmen nicht mit der Richtung überein
   Kontur, dann wird ihnen ein Vorzeichen vorangestellt
   «-».

Zum Beispiel,
für die Kontur von Abb. 18 das zweite Kirchhoffsche Gesetz
wird wie folgt geschrieben:

U₁
– u₂
+ u₃
= E₁
–E₃
–E₄
(21)

Gleichung (20) sein kann
umschreiben als:

 (Ui
– Ei)
= 0 (22)

Wo
(u
– E)
- Spannung am Ast.

Folglich,
Das zweite Kirchhoffsche Gesetz kann formuliert werden
auf die folgende Weise:

Algebraisch
die Summe der Spannungen an den Zweigen in jedem
geschlossene Schleife ist Null.

Potenzial
das zuvor besprochene Diagramm dient
grafische Interpretation des zweiten
Kirchhoffsches Gesetz.

Aufgabe Nummer 1.

BEI
Die Schaltung in Abb. 1 erhält Ströme I₁
und ich₃,
Widerstand und EMK Ströme bestimmen
ich₄,
ich₅,
ich₆
; Spannung zwischen den Punkten a
und B
wenn ich₁
= 10mA,
ich₃
= -20 mA,
R₄
= 5kOhm,
E₅
= 20B,
R₅
= 3 kOhm,
E₆
= 40B,
R₆
= 2kOhm.

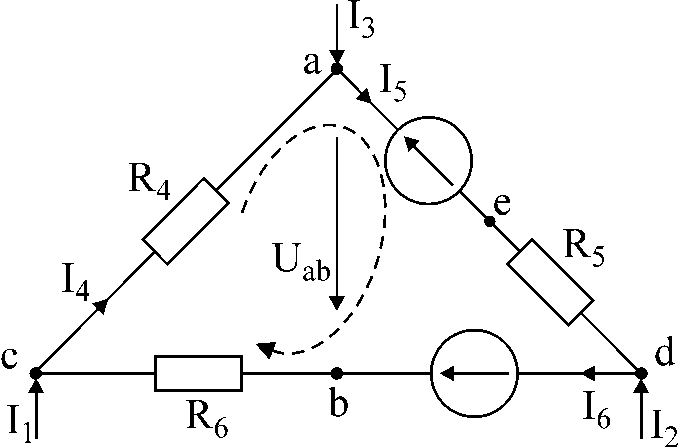
Abb.1

Lösung:

1. Für ein gegebenes
   Kontur, wir komponieren zwei Gleichungen gemäß
   Kirchhoffs erstes Gesetz und ein - gem
   zweite. Konturrichtung
   durch einen Pfeil angedeutet.

BEI
als Ergebnis der Lösung erhalten wir: I₆
= 0; ich₄
= 10mA;
ich₅
= -10mA

1. Fragen
   Spannungsrichtung zwischen den Punkten
   a
   und B
   ab Punkt "a"
   zu Punkt "b"
   — u_ab.
   Diese Spannung kann aus der Gleichung gefunden werden
   Kirchhoffs zweites Gesetz:

ich₄R₄
+ u_ab
+ ich₆R₆
= 0

U_ab
= - 50 V.

Aufgabe Nummer 2.

Zum
Diagramme in Abb. 2 Gleichungen aufstellen gem
Kirchhoffschen Gesetze und bestimmen die Unbekannten
Punkte.

Gegeben:
ich₁
= 20mA;
ich₂
= 10mA

R₁
= 5kOhm,
R₃
= 4 kOhm,
R₄
= 6kOhm,
R₅
= 2kOhm,
R₆
= 4kΩ.

Abb.2

Lösung:

Anzahl der Knoten
Gleichungen - 3, die Anzahl der Konturgleichungen
– 1.

Denken Sie daran!
Beim Erstellen der Gleichung nach dem zweiten
Kirchhoffsches Gesetz, wir wählen die Kontur, in
die keine Stromquellen enthält.
Die Richtung der Kontur ist in der Figur angegeben.

BEI
dieser Schaltung die Ströme der Zweige I₁
und ich₂.
Unbekannt
Strömungen
ich₃,
ich₄,
ich₅,
ich₆.

Entscheiden
System erhalten wir: I₃
= 13,75 mA;
ich₄
= -3,75 mA;
ich₅
= 6,25 mA;
ich₆
= 16,25 mA.

Grundlegendes Konzept

Elektrischer Strom fließt, wenn ein geschlossener Stromkreis es Elektronen ermöglicht, sich von einem hohen Potential zu einem niedrigeren im Stromkreis zu bewegen. Mit anderen Worten, der Strom erfordert eine Elektronenquelle, die die Energie hat, sie in Bewegung zu setzen, sowie einen Punkt ihrer Rückkehr negativer Ladungen, der durch ihren Mangel gekennzeichnet ist. Als physikalisches Phänomen wird der Strom in einem Stromkreis durch drei grundlegende Größen charakterisiert:

• Stromspannung;
• Stromstärke;
• der Widerstand eines Leiters, durch den sich Elektronen bewegen.

Kraft und Spannung

Die Stromstärke (I, gemessen in Ampere) ist das Volumen der Elektronen (Ladung), die sich pro Zeiteinheit durch eine Stelle im Stromkreis bewegen. Mit anderen Worten, Messung I ist die Bestimmung der Anzahl der sich bewegenden Elektronen

Es ist wichtig zu verstehen, dass sich der Begriff nur auf Bewegung bezieht: Statische Ladungen, beispielsweise an den Anschlüssen einer nicht angeschlossenen Batterie, haben keinen messbaren Wert von I. Strom, der in eine Richtung fließt, wird als Gleichstrom (DC) und bezeichnet periodisch wechselnde Richtungen werden als alternierend (AC) bezeichnet. Spannung kann durch ein Phänomen wie Druck oder als Unterschied in der potentiellen Energie von Objekten unter dem Einfluss der Schwerkraft dargestellt werden

Um dieses Ungleichgewicht zu erzeugen, müssen Sie zunächst Energie aufwenden, die unter geeigneten Umständen in Bewegung umgesetzt wird. Beispielsweise wird beim Fallen einer Last aus großer Höhe gearbeitet, um sie anzuheben, in galvanischen Batterien entsteht die Potentialdifferenz an den Klemmen durch Umwandlung chemischer Energie, in Generatoren - als Folge der Einwirkung von ein elektromagnetisches Feld

Stress kann durch ein Phänomen wie Druck oder als Unterschied in der potentiellen Energie von Objekten unter dem Einfluss der Schwerkraft veranschaulicht werden. Um dieses Ungleichgewicht zu erzeugen, müssen Sie zunächst Energie aufwenden, die unter geeigneten Umständen in Bewegung umgesetzt wird. Beispielsweise wird beim Herunterfallen einer Last aus großer Höhe die Arbeit des Anhebens verwirklicht, in galvanischen Batterien entsteht die Potentialdifferenz an den Klemmen durch Umwandlung chemischer Energie, in Generatoren - als Folge der Einwirkung von elektromagnetisches Feld.

Leiterwiderstand

Egal wie gut ein gewöhnlicher Leiter ist, er wird Elektronen niemals ohne einen gewissen Widerstand gegen ihre Bewegung passieren lassen. Es ist möglich, den Widerstand als Analogon zur mechanischen Reibung zu betrachten, obwohl dieser Vergleich nicht perfekt sein wird.Wenn Strom durch einen Leiter fließt, wird eine gewisse Potentialdifferenz in Wärme umgewandelt, sodass am Widerstand immer ein Spannungsabfall auftritt. Elektroheizungen, Haartrockner und ähnliche Geräte sind ausschließlich dazu bestimmt, elektrische Energie in Form von Wärme abzugeben.

Der vereinfachte Widerstand (als R bezeichnet) ist ein Maß dafür, wie stark der Elektronenfluss in einem Stromkreis verzögert wird. Es wird in Ohm gemessen. Die Leitfähigkeit eines Widerstands oder eines anderen Elements wird durch zwei Eigenschaften bestimmt:

• Geometrie;
• Material.

Die Form ist von größter Bedeutung, wie aus der hydraulischen Analogie hervorgeht: Wasser durch ein langes und schmales Rohr zu schieben ist viel schwieriger als Wasser durch ein kurzes und breites zu schieben. Materialien spielen eine entscheidende Rolle. Beispielsweise können sich Elektronen in einem Kupferdraht frei bewegen, aber überhaupt nicht durch Isolatoren wie Gummi fließen, unabhängig von ihrer Form. Neben Geometrie und Material gibt es weitere Faktoren, die die Leitfähigkeit beeinflussen.

Interpretation des Ohmschen Gesetzes

Um die Ladungsbewegung sicherzustellen, müssen Sie den Stromkreis schließen. Ohne zusätzliche Leistung kann der Strom nicht lange bestehen. Potenziale werden schnell gleich. Um den Betriebsmodus der Schaltung aufrechtzuerhalten, wird eine zusätzliche Quelle (Generator, Batterie) benötigt.

Der komplette Stromkreis enthält den gesamten elektrischen Widerstand aller Komponenten. Für genaue Berechnungen werden Verluste in Leitern, Widerstandselementen und einer Stromquelle berücksichtigt.

Wie viel Spannung für eine bestimmte Stromstärke angelegt werden muss, errechnet sich aus der Formel:

U=I*R.

In ähnlicher Weise werden mit Hilfe der betrachteten Beziehungen andere Parameter der Schaltung bestimmt.

Parallele und serielle Verbindung

In der Elektrik werden Elemente entweder in Reihe geschaltet - nacheinander oder parallel - das heißt, wenn mehrere Eingänge mit einem Punkt verbunden sind und Ausgänge von denselben Elementen mit einem anderen verbunden sind.

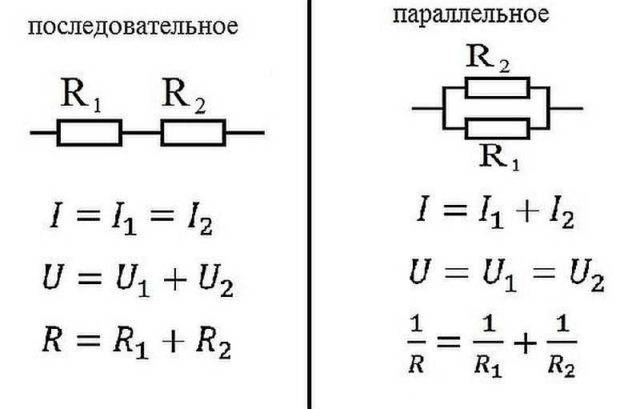
Ohmsches Gesetz für Parallel- und Reihenschaltung

serielle Verbindung

Wie funktioniert das Ohmsche Gesetz für diese Fälle? Bei einer Reihenschaltung ist der durch die Elementkette fließende Strom derselbe. Die Spannung eines Abschnitts eines Stromkreises mit in Reihe geschalteten Elementen wird als Summe der Spannungen in jedem Abschnitt berechnet. Wie lässt sich das erklären? Der Stromfluss durch ein Element ist die Übertragung eines Teils der Ladung von einem Teil auf einen anderen. Ich meine, es ist etwas Arbeit. Die Größe dieser Arbeit ist Spannung. Das ist die physikalische Bedeutung von Stress. Wenn das klar ist, fahren wir fort.

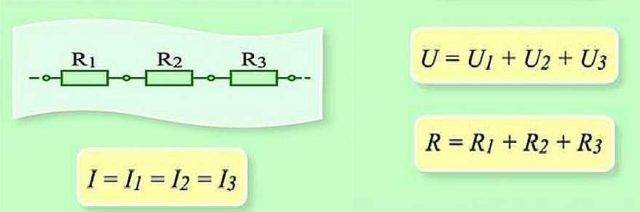
Serielle Verbindung und Parameter dieses Abschnitts der Schaltung

Bei einer Reihenschaltung muss die Ladung der Reihe nach durch jedes Element übertragen werden. Und für jedes Element ist dies ein gewisses „Arbeitsvolumen“. Und um den Arbeitsaufwand für den gesamten Abschnitt der Kette zu finden, müssen Sie die Arbeit für jedes Element hinzufügen. Es stellt sich also heraus, dass die Gesamtspannung die Summe der Spannungen an jedem der Elemente ist.

Auf die gleiche Weise wird – mit Hilfe der Addition – auch der Gesamtwiderstand des Schaltungsabschnitts ermittelt. Wie kann man sich das vorstellen? Der durch die Elementkette fließende Strom überwindet sequentiell alle Widerstände. Einer nach dem anderen. Das heißt, um den Widerstand zu finden, den er überwunden hat, ist es notwendig, die Widerstände zu addieren. Ungefähr so. Die mathematische Ableitung ist komplizierter und der Mechanismus dieses Gesetzes ist leichter zu verstehen.

Parallele Verbindung

Eine Parallelschaltung liegt vor, wenn die Anfänge der Leiter / Elemente an einem Punkt zusammenlaufen und an einem anderen ihre Enden verbunden sind. Wir werden versuchen, die Gesetzmäßigkeiten zu erklären, die für solche Verbindungen gelten. Beginnen wir mit dem Strom. Dem Verbindungspunkt der Elemente wird ein Strom einer gewissen Größe zugeführt. Es trennt sich und fließt durch alle Leiter. Daraus schließen wir, dass der Gesamtstrom im Abschnitt gleich der Summe des Stroms in jedem der Elemente ist: I = I1 + I2 + I3.

Nun zur Spannung. Wenn Spannung Arbeit ist, um eine Ladung zu bewegen, dann ist die Arbeit, die zum Bewegen einer Ladung benötigt wird, bei jedem Element gleich. Das heißt, die Spannung an jedem parallel geschalteten Element ist gleich. U=U1=U2=U3. Nicht so lustig und anschaulich wie bei der Erklärung des Ohmschen Gesetzes für einen Kettenabschnitt, aber man kann es verstehen.

Gesetze für die Parallelschaltung

Beim Widerstand sind die Dinge etwas komplizierter. Lassen Sie uns das Konzept der Leitfähigkeit einführen. Dies ist ein Merkmal, das angibt, wie leicht oder schwer es für eine Ladung ist, diesen Leiter zu passieren. Es ist klar, dass je niedriger der Widerstand ist, desto leichter wird es für den Strom passieren. Daher wird die Leitfähigkeit - G - als Kehrwert des Widerstands berechnet. In der Formel sieht das so aus: G = 1/R.

Warum sprechen wir von Leitfähigkeit? Denn die Gesamtleitfähigkeit eines Abschnitts mit einer Parallelschaltung von Elementen ist gleich der Summe der Leitfähigkeit für jeden der Abschnitte. G = G1 + G2 + G3 - leicht verständlich. Wie leicht der Strom diesen Knoten paralleler Elemente überwinden kann, hängt von der Leitfähigkeit jedes der Elemente ab. Es stellt sich also heraus, dass sie gefaltet werden müssen.

Jetzt können wir zum Widerstand übergehen. Da die Leitfähigkeit der Kehrwert des Widerstands ist, können wir die folgende Formel erhalten: 1/R = 1/R1 + 1/R2 + 1/R3.

Was gibt uns eine parallele und serielle Verbindung?

Theoretisches Wissen ist gut, aber wie wendet man es in der Praxis an? Elemente beliebiger Art können parallel und in Reihe geschaltet werden. Aber wir haben nur die einfachsten Formeln betrachtet, die lineare Elemente beschreiben. Lineare Elemente sind Widerstände, die auch „Widerstände“ genannt werden. So können Sie das Gelernte anwenden:

Steht kein großohmiger Widerstand zur Verfügung, sondern mehrere kleinere, kann der gewünschte Widerstand durch Reihenschaltung mehrerer Widerstände erreicht werden. Wie Sie sehen können, ist dies ein nützlicher Trick.
Um die Lebensdauer der Batterien zu verlängern, können sie parallel geschaltet werden. In diesem Fall bleibt die Spannung nach dem Ohmschen Gesetz gleich (Sie können dies überprüfen, indem Sie die Spannung mit einem Multimeter messen). Und die „Lebensdauer“ einer Doppelbatterie ist viel länger als die von zwei Elementen, die sich gegenseitig ersetzen

Achtung: Es dürfen nur Netzteile mit gleichem Potential parallel geschaltet werden. Das heißt, eine leere und eine neue Batterie können nicht angeschlossen werden.

Wenn Sie immer noch eine Verbindung herstellen, lädt der Akku mit einer höheren Ladung tendenziell einen weniger geladenen auf. Als Ergebnis sinkt ihre Gesamtladung auf einen niedrigen Wert.

Im Allgemeinen sind dies die häufigsten Verwendungen für diese Verbindungen.

Ideale EMF-Quelle

Die elektromotorische Kraft (E) ist eine physikalische Größe, die den Grad des Einflusses äußerer Kräfte auf die Bewegung in einem geschlossenen Kreislauf von Ladungsträgern bestimmt. Mit anderen Worten, wie stark der Strom dazu neigt, durch den Leiter zu fließen, hängt von der EMF ab.

Bei der Erklärung solch unverständlicher Phänomene greifen Hausschullehrer gerne auf die Methode der hydraulischen Analogien zurück.Wenn ein Leiter ein Rohr ist und elektrischer Strom die Menge an Wasser, die durch ihn fließt, dann ist EMF der Druck, den eine Pumpe entwickelt, um Flüssigkeit zu pumpen.

Der Begriff elektromotorische Kraft bezieht sich auf ein solches Konzept wie Spannung. Sie, EMF, wird auch in Volt gemessen (Einheit - "V"). Jede Energiequelle, sei es eine Batterie, ein Generator oder ein Solarpanel, hat ihre eigene elektromotorische Kraft. Oft liegt diese EMK nahe der Ausgangsspannung (U), aber immer etwas darunter. Dies wird durch den Innenwiderstand der Quelle verursacht, an dem zwangsläufig ein Teil der Spannung abfällt.

Aus diesem Grund ist die ideale Quelle für EMF eher ein abstraktes Konzept oder ein physikalisches Modell, das in der realen Welt keinen Platz hat, da der Innenwiderstand der Batterie Rin, obwohl sehr niedrig, immer noch vom absoluten Nullpunkt verschieden ist.

Ideale und echte EMK-Quelle

In differentieller Form

Die Formel wird sehr oft in differentieller Form dargestellt, da der Leiter meist inhomogen ist und in möglichst kleine Abschnitte zerlegt werden muss. Dem durchfließenden Strom werden Größe und Richtung zugeordnet, sodass er als skalare Größe betrachtet wird. Immer wenn der resultierende Strom durch eine Leitung ermittelt werden soll, wird die algebraische Summe aller Einzelströme gebildet. Da diese Regel nur für skalare Größen gilt, wird auch der Strom als skalare Größe genommen. Es ist bekannt, dass der Strom dI = jdS durch den Abschnitt fließt. Die Spannung darauf ist Edl, dann gilt für einen Draht mit konstantem Querschnitt und gleicher Länge das Verhältnis:

Differentialform

Daher lautet der Ausdruck des Stroms in Vektorform: j = E.

Wichtig! Bei metallischen Leitern nimmt die Leitfähigkeit mit steigender Temperatur ab, bei Halbleitern nimmt sie zu. Omovs Gesetz zeigt keine strikte Verhältnismäßigkeit

Der Widerstand einer großen Gruppe von Metallen und Legierungen verschwindet bei einer Temperatur nahe dem absoluten Nullpunkt, und der Vorgang wird als Supraleitung bezeichnet.